Problemas de Mecánica para Olimpiada
DOI: https://doi.org/10.31644/IMASD.28.2021.a09 Publicación: 01 octubre 2021
Resumen
Estas notas contienen una colección breve de problemas de mecánica clásica newtoniana pensados para el entrenamiento en Olimpiadas de Física de la selección nacional mexicana de 2020 que represento a México en olimpiadas internacionales, sumándose así a colecciones similares que ya existen. Algunos problemas fueron recopilados de fuentes clásicas como problemarios u otras olimpiadas y son bien conocidos, otros los he modificado o inventado para formar una colección que incluya problemas originales en el espíritu de la (hoy extinta) Editorial Mir y el estilo de problemas de Olimpiada de Física de la “vieja escuela”. Las respuestas a los problemas se dan al final del texto con diferentes grados de detalle en la resolución, mientras que en algunos casos se dan soluciones completas en otros se muestra únicamente la respuesta. Esto es intencional y tiene como propósito incentivar al lector a encontrar soluciones propias y originales a los problemas propuestos que se presentan así como un reto en el proceso de aprendizaje. Siguiendo la tradición de los problemas de olimpiadas se han propuesto problemas elementales, pero no sencillos. Esta breve colección de problemas también podría ser de utilidad como material complementario en cursos de mecánica clásica en el nivel superior.
Quiero agradecer a Dalí Pinto y Jairo Villalobos, estudiantes de la licenciatura en Física de la Universidad Autónoma de Chiapas, por ayudarme a elaborar las figuras y diagramas, así como por interminables discusiones de problemas de física y matemáticas. Aunque el manuscrito ha sido revisado en varias ocasiones cualquier error que subsista en el mismo es responsabilidad mía, y por esto apelo a los lectores que si encontraran errores me lo hicieran saber al correo idrish.huet@gmail.com a fin de que pudieran corregirse en una versión posterior.
Espero que estos problemas sean interesantes para los estudiantes de olimpiadas y tan interesantes y útiles en esta etapa de su aprendizaje de la física, como en su momento otras colecciones similares de problemas lo fueron para mí.

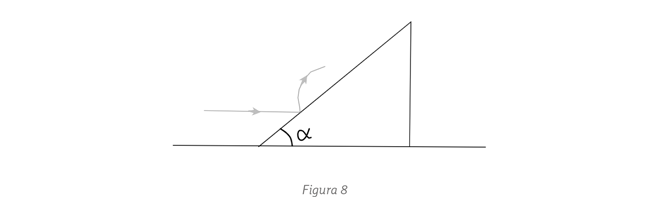
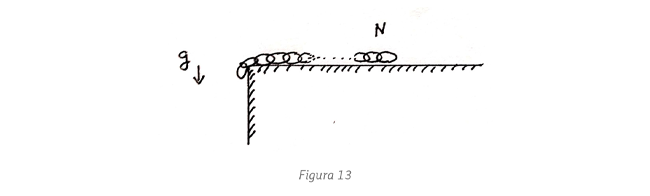
 en el momento en que el
bloque y la barra se separan? (b) Calcula la velocidad del bloque cuando esto ocurre.
en el momento en que el
bloque y la barra se separan? (b) Calcula la velocidad del bloque cuando esto ocurre.
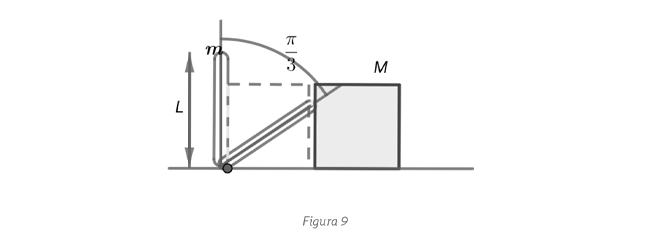
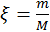 para los cuales ocurre un segundo choque entre las masas
para los cuales ocurre un segundo choque entre las masas 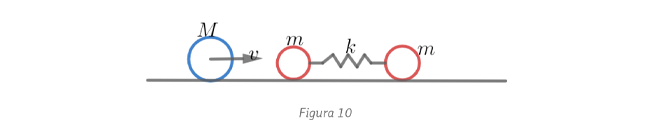
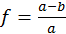 y cumple
y cumple
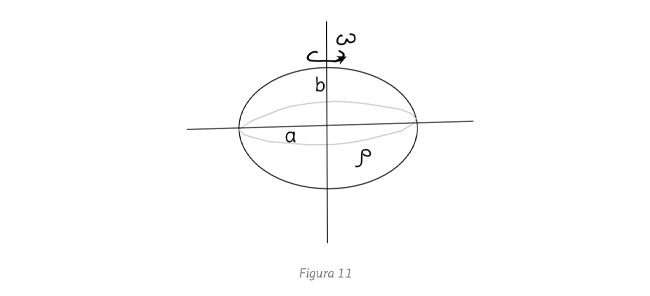
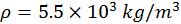 y compara el resultado con el valor real
y compara el resultado con el valor real 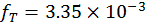 . Por simplicidad asume que la fuerza gravitacional
puede calcularse para este elipsoide concibiendo toda la masa como concentrada en el centro de masas.
. Por simplicidad asume que la fuerza gravitacional
puede calcularse para este elipsoide concibiendo toda la masa como concentrada en el centro de masas.
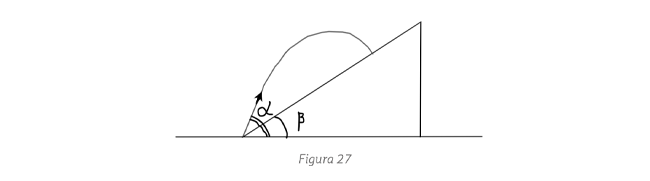
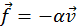 , la resistencia del aire lo frena de manera que terminara estrellándose contra la Tierra. Originalmente orbita a una altura sobre la superficie igual a la mitad del radio terrestre y que la caída del satélite ocurre
lentamente. ¿Cuantas vueltas dará a la tierra el satélite antes de impactarse?
, la resistencia del aire lo frena de manera que terminara estrellándose contra la Tierra. Originalmente orbita a una altura sobre la superficie igual a la mitad del radio terrestre y que la caída del satélite ocurre
lentamente. ¿Cuantas vueltas dará a la tierra el satélite antes de impactarse?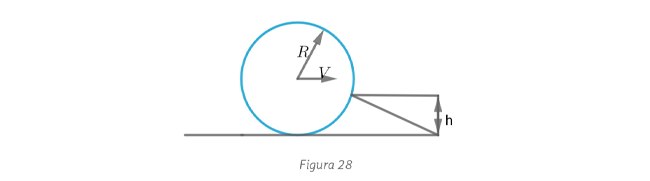
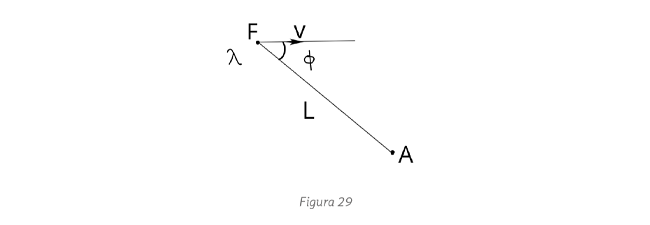
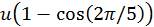 . De aquí resulta
. De aquí resulta 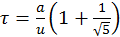 .
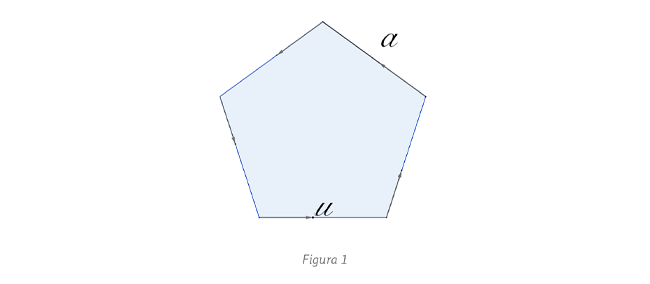
Otra forma consiste en descomponer el movimiento de cada hormiga de forma instantánea en una rotación respecto al centro del pentágono y un escalamiento del pentágono (velocidad radial), usando este método es posible también demostrar
que las hormigas se mueven siguiendo una espiral logarítmica.
.
Otra forma consiste en descomponer el movimiento de cada hormiga de forma instantánea en una rotación respecto al centro del pentágono y un escalamiento del pentágono (velocidad radial), usando este método es posible también demostrar
que las hormigas se mueven siguiendo una espiral logarítmica.
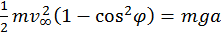 con
con 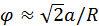 .
Resulta
.
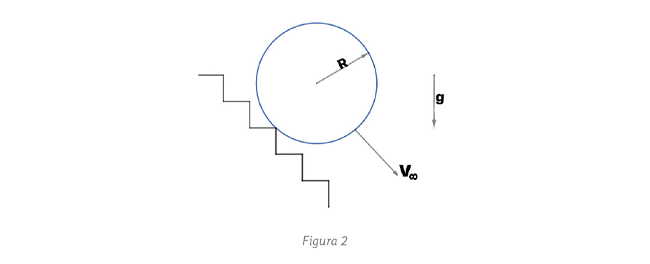
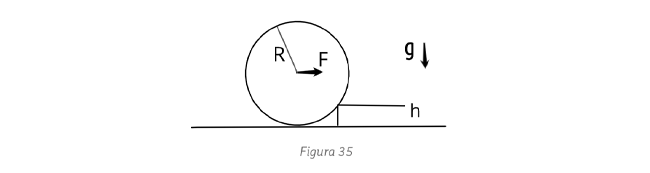
Resulta 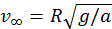 (b) En este caso la esfera va girando al caer y se debe considerar la energía cinética
de rotación, si
(b) En este caso la esfera va girando al caer y se debe considerar la energía cinética
de rotación, si 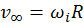 tenemos
tenemos 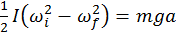 , donde
, donde 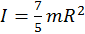 . La conservación del momento angular implica
. La conservación del momento angular implica 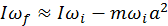 de aquí resulta
de aquí resulta 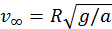 . En el caso (b) las fuerzas de fricción no realizan trabajo, por esto el resultado es el mismo para v∞.
. En el caso (b) las fuerzas de fricción no realizan trabajo, por esto el resultado es el mismo para v∞.
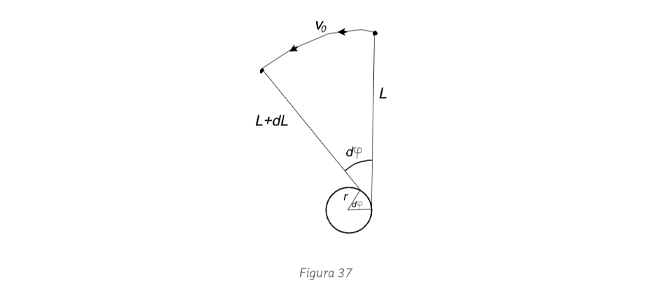
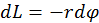 , y en cada instante
, y en cada instante 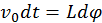 , resulta
, resulta 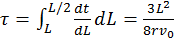 .
.
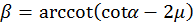 si
si 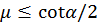 ,
, 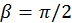 si
si 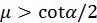 .
. . (b) Aquí hay que usar las ecuaciones de movimiento
para cuerpo rígido. La aceleración angular resulta
. (b) Aquí hay que usar las ecuaciones de movimiento
para cuerpo rígido. La aceleración angular resulta 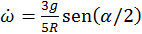 , y la fuerza de fricción
, y la fuerza de fricción 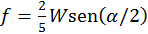 , de esto resulta
, de esto resulta
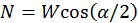 . (c) En este caso la aceleración del centro de masas de la esfera es
. (c) En este caso la aceleración del centro de masas de la esfera es 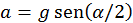 , resulta
, resulta 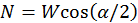 .
.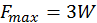 . (b)
. (b) 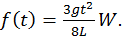 para
para 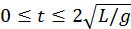 ,
, 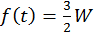 para
para 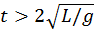 . (c)
. (c) 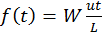 para
para 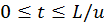 ,
, 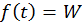 para
para 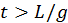 . (d) La tensión en cada caso es:
. (d) La tensión en cada caso es: 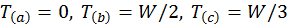 .
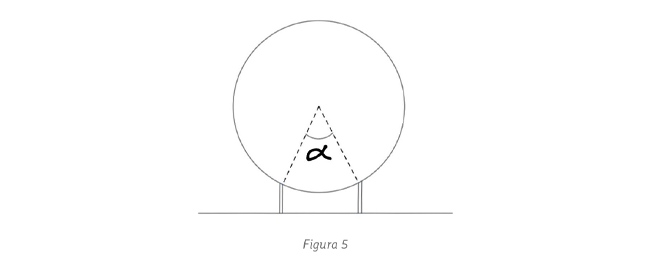
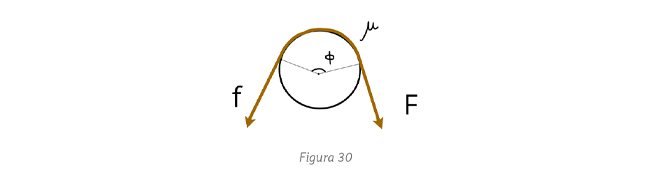
.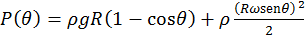 (b) La presión máxima
(b) La presión máxima 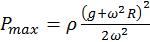 ocurre en .
ocurre en .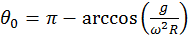 si
si 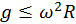 , y
, y 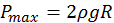 en
en 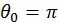 si
si 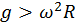 .
.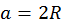 , usando las tres leyes de Kepler:
, usando las tres leyes de Kepler:
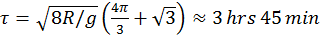 .
.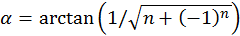 .
.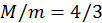 . (b)
. (b) 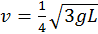
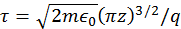
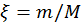 habrá un segundo choque siempre que exista solución a la ecuación trascendental
habrá un segundo choque siempre que exista solución a la ecuación trascendental 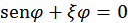 . Aproximadamente
. Aproximadamente 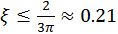 .
.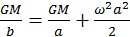 . Resulta
. Resulta 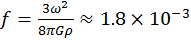 (En realidad esta aproximación es incorrecta por un factor 5/2 debido a la suposición dada para simplificar. I. Newton calculó por primera vez el resultado correcto.)
(En realidad esta aproximación es incorrecta por un factor 5/2 debido a la suposición dada para simplificar. I. Newton calculó por primera vez el resultado correcto.)
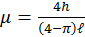
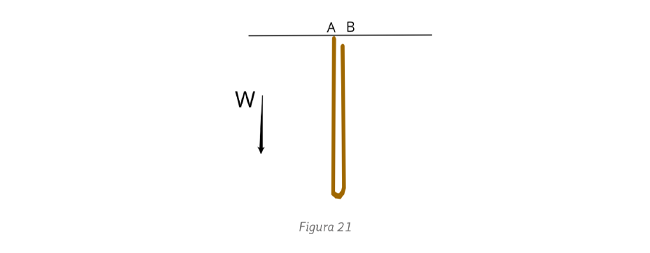
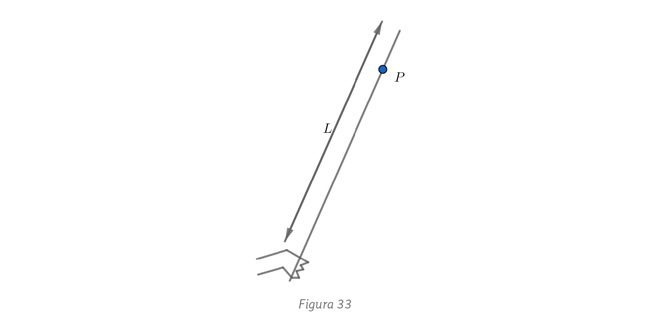
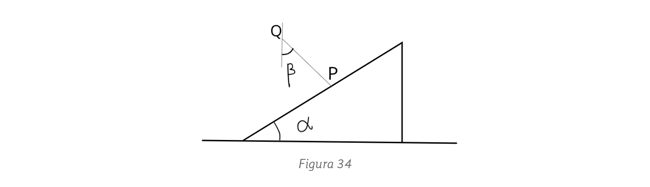
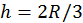 arriba de su centro.
arriba de su centro.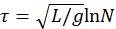
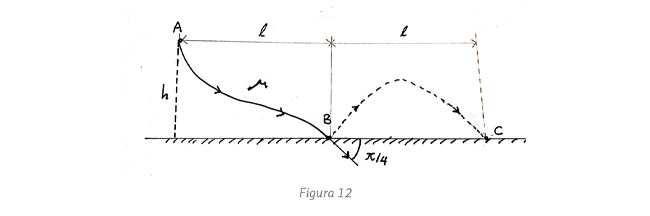
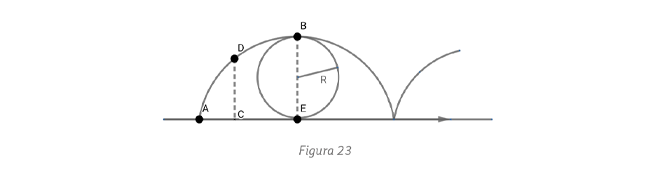
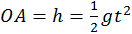 la componente de la gravedad que acelera
las cuentas nos dice que la curva obedece
la componente de la gravedad que acelera
las cuentas nos dice que la curva obedece
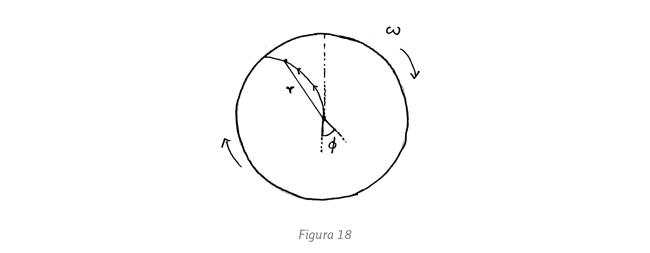
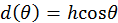 (esto ya implica que
(esto ya implica que 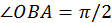 ). Esta curva es una circunferencia de diámetro h, pues como se ve en el diagrama I:
). Esta curva es una circunferencia de diámetro h, pues como se ve en el diagrama I: 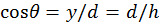 ,
luego
,
luego 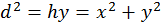 . Que resulta en
. Que resulta en 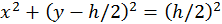 .
.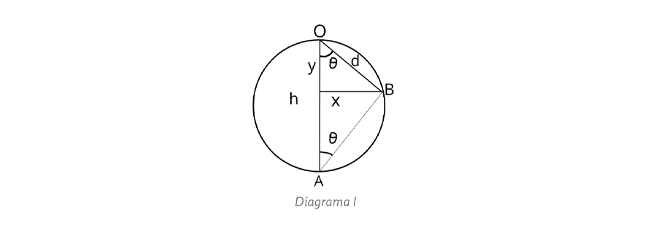
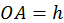 ,
, 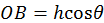 (esto ya implica que
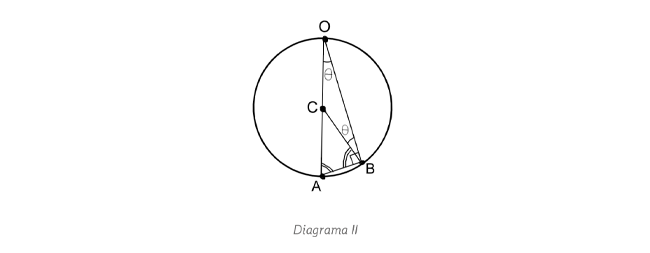
(esto ya implica que 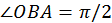 ). Sea C el punto en OA tal que CB bisecta
). Sea C el punto en OA tal que CB bisecta
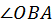 entonces
entonces 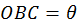 y OBC es isósceles. También ABC es isósceles. Entonces
y OBC es isósceles. También ABC es isósceles. Entonces 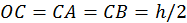 , por esto
todo punto B equidista de C.
, por esto
todo punto B equidista de C.
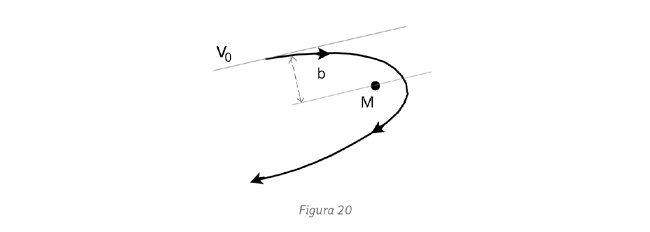
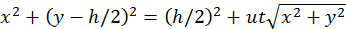 , sino una limaçon (caracol) de Pascal, en coordenadas
polares:
, sino una limaçon (caracol) de Pascal, en coordenadas
polares: 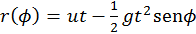
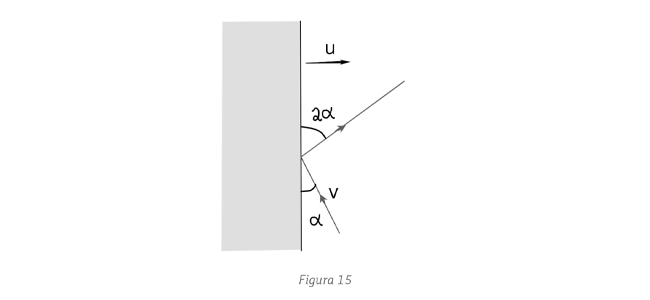
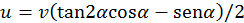 . (b)
. (b) 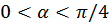 .
.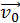 . (b) Recorre más distancia cuando va girando.
. (b) Recorre más distancia cuando va girando.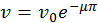
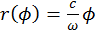
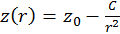
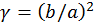
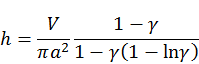
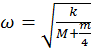
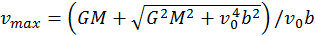
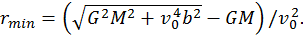
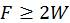
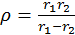 . (b)
. (b) 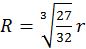
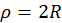
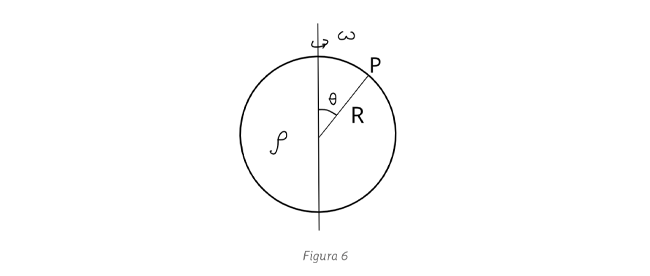
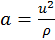 tiene tres contribuciones en ese sistema la centrípeta, la
del potencial centrifugo y la de Coriolis:
tiene tres contribuciones en ese sistema la centrípeta, la
del potencial centrifugo y la de Coriolis:
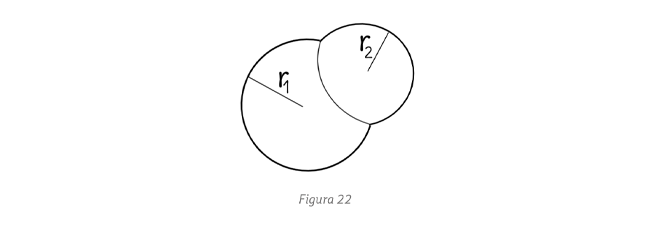
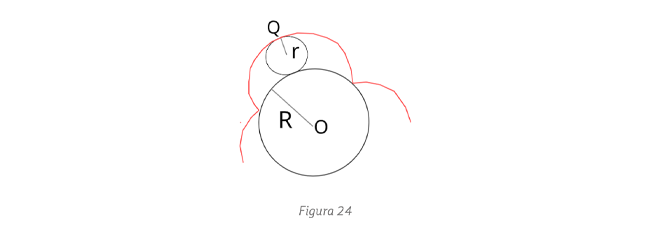
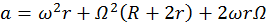 , respectivamente, donde Ω es la velocidad angular del centro de la circunferencia de radio r alrededor de la de radio R y ω es la velocidad angular de rotación de la circunferencia de radio r. La condición de rodamiento sin deslizamiento es
, respectivamente, donde Ω es la velocidad angular del centro de la circunferencia de radio r alrededor de la de radio R y ω es la velocidad angular de rotación de la circunferencia de radio r. La condición de rodamiento sin deslizamiento es 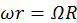 .
. 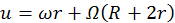 es la velocidad del punto generador en el sistema O′.
es la velocidad del punto generador en el sistema O′. 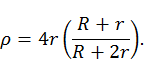
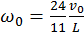 . (b)
. (b) 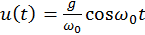 . (c)
. (c) 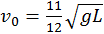
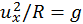 , usando conservación de la energía,
, usando conservación de la energía,
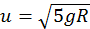 . (b)
. (b) 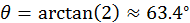 .
.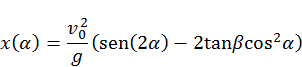
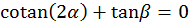 , de donde se obtiene
, de donde se obtiene
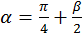 .
.
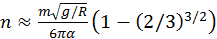
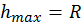 . (b)
. (b) 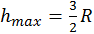
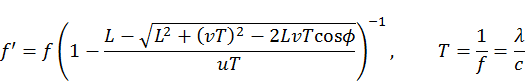
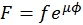
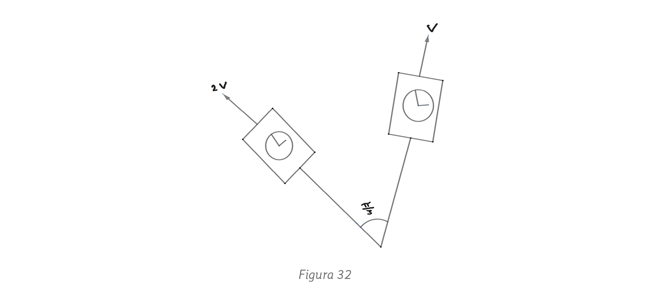
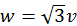 , y debe ser igual además a
, y debe ser igual además a 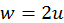 donde
donde 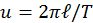 es la velocidad de la punta del segundero y T = 1 min . Además
es la velocidad de la punta del segundero y T = 1 min . Además 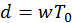 donde
donde 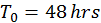
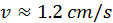 ,
, 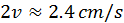 . (b)
. (b) 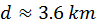
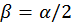 .
.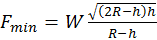 .
.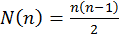 . (b)
. (b) 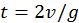 . Claramente para que dicho evento ocurra se requiere
. Claramente para que dicho evento ocurra se requiere  . (c) Enumerando a las velocidades
como
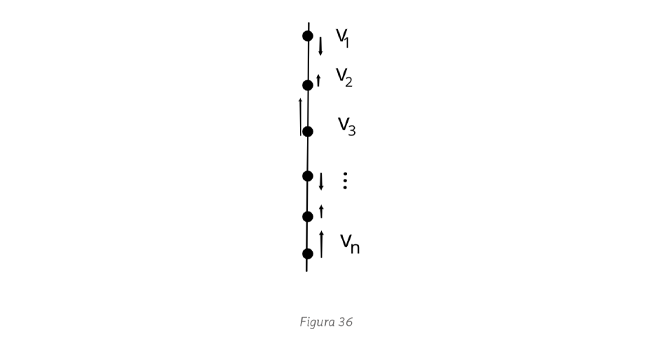
. (c) Enumerando a las velocidades
como 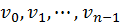 , de manera que
, de manera que 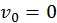 sea la velocidad de la cuenta más abajo, una elección posible (no es la única) es
sea la velocidad de la cuenta más abajo, una elección posible (no es la única) es 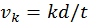 para
para 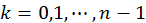 .
.